Problemas envolvendo números inteiros
Problemas envolvendo números inteiros
1- Uma barata andou sobre uma trena da marcação de 6 polegadas até a marcação de
20 polegadas, fazendo uma parada na metade do trecho. Em que posição da trena ocorreu essa parada?
 Resposta: 13 poleadas
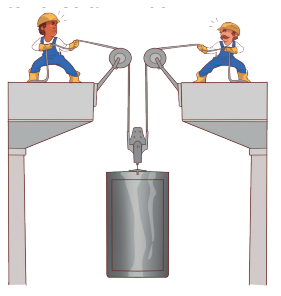
2. Em um porto, dois homens estão erguendo um contêiner com o auxílio de um sistema
de cabos e roldanas, como mostra a figura a seguir. Se um deles puxar 15 metros de cabo, e o outro puxar 25 metros, quantos metros o contêiner será erguido?
Resposta: 13 poleadas
2. Em um porto, dois homens estão erguendo um contêiner com o auxílio de um sistema
de cabos e roldanas, como mostra a figura a seguir. Se um deles puxar 15 metros de cabo, e o outro puxar 25 metros, quantos metros o contêiner será erguido?
 Resolução: Sabendo que temos dois operários puxando o contêiner faremos o seguinte chamaremos os dois operários de “2x” sendo que um
x= 15 metros e o outro operário de x= 25 metros. Vamos somar os dois ai teremos 2x = 40 metros. Agora dividiremos por dois a equação:
x = 40 / 2 que dará x = 20 metros. Essa é a resposta, 20 metros.
3. Em uma competição de sinuca com quatro duplas participantes, cada dupla jogava uma
vez contra cada uma das outras duplas. Se um confronto acabasse empatado, cada equipe
receberia 1 ponto; do contrário, a dupla vencedora receberia 3 pontos, e a perdedora não pontuaria. A seguir, temos a tabela que mostra o total de pontos obtidos pelas duplas após todos
os confrontos:
Resolução: Sabendo que temos dois operários puxando o contêiner faremos o seguinte chamaremos os dois operários de “2x” sendo que um
x= 15 metros e o outro operário de x= 25 metros. Vamos somar os dois ai teremos 2x = 40 metros. Agora dividiremos por dois a equação:
x = 40 / 2 que dará x = 20 metros. Essa é a resposta, 20 metros.
3. Em uma competição de sinuca com quatro duplas participantes, cada dupla jogava uma
vez contra cada uma das outras duplas. Se um confronto acabasse empatado, cada equipe
receberia 1 ponto; do contrário, a dupla vencedora receberia 3 pontos, e a perdedora não pontuaria. A seguir, temos a tabela que mostra o total de pontos obtidos pelas duplas após todos
os confrontos:
 Quantos confrontos terminaram empatados?
Vamos lá…para responder essa questão primeiramente precisamos saber o número total de partida, os possíveis resultados para cada equipe e o total de pontos para cada resultado. Depois precisamos comparar a pontuação total da tabela que é 13 pontos somados os ( 5 + 3 + 3 + 2 ) = 13 pontos e logo após comparar com a pontuação das possíveis situação onde temos empates, vitórias e derrotas.
Quantos confrontos terminaram empatados?
Vamos lá…para responder essa questão primeiramente precisamos saber o número total de partida, os possíveis resultados para cada equipe e o total de pontos para cada resultado. Depois precisamos comparar a pontuação total da tabela que é 13 pontos somados os ( 5 + 3 + 3 + 2 ) = 13 pontos e logo após comparar com a pontuação das possíveis situação onde temos empates, vitórias e derrotas.  Número 1: total de confrontos 6 partidas.
agora vamos partir para o Número 2: Possíveis resultados para cada equipe
Número 1: total de confrontos 6 partidas.
agora vamos partir para o Número 2: Possíveis resultados para cada equipe agora que sabemos os números possíveis de resultados para cada equipe somamos os pontos. Veja os exemplos ao lado. primeiro temos os possíveis resultados de três vitórias para uma determinada equipe logo essa equipe faturaria 3 pontos por cada vitória dando um total de 9 pontos. Também temos o resultado de três derrotas dando um total de zero pontos. Temos também o resultado de três empates dando um total de 3 pontos pois cada empate lhe daria 1 ponto…e assim montamos os diversos resultados possíveis como você pode vê ao lado.
Número 3: Comparamos os possíveis resultados com os resultados da tabela das equipes e excluímos alguns resultados.
agora que sabemos os números possíveis de resultados para cada equipe somamos os pontos. Veja os exemplos ao lado. primeiro temos os possíveis resultados de três vitórias para uma determinada equipe logo essa equipe faturaria 3 pontos por cada vitória dando um total de 9 pontos. Também temos o resultado de três derrotas dando um total de zero pontos. Temos também o resultado de três empates dando um total de 3 pontos pois cada empate lhe daria 1 ponto…e assim montamos os diversos resultados possíveis como você pode vê ao lado.
Número 3: Comparamos os possíveis resultados com os resultados da tabela das equipes e excluímos alguns resultados.  Agora vamos excluir e ficar apenas com os resultados que possui o total de pontos para cada equipe. Exemplo: a equipe “A” possui 5 pontos, então só existe uma possibilidade de resultado para esta equipe que seria uma vitória e dois empates. A mesma coisa seria para a equipe “D” que possui 2 pontos, então a única situação que lhe daria esses dois pontos seria dois empates e uma derrota e assim por diante.
Número 4: Vamos agora montar uma tabela com os possíveis pontos e comparar o total de partidas com o total possível de empates. Por exemplo: se todas as equipes empassem então elas só teriam ganhado um ponto por partida e teriam no final de uma rodada um total de 3 pontos cada equipe.
Agora vamos excluir e ficar apenas com os resultados que possui o total de pontos para cada equipe. Exemplo: a equipe “A” possui 5 pontos, então só existe uma possibilidade de resultado para esta equipe que seria uma vitória e dois empates. A mesma coisa seria para a equipe “D” que possui 2 pontos, então a única situação que lhe daria esses dois pontos seria dois empates e uma derrota e assim por diante.
Número 4: Vamos agora montar uma tabela com os possíveis pontos e comparar o total de partidas com o total possível de empates. Por exemplo: se todas as equipes empassem então elas só teriam ganhado um ponto por partida e teriam no final de uma rodada um total de 3 pontos cada equipe. Se nós somássemos o total de pontos de todas as equipes juntas teríamos um total de 12 pontos. Conclusão: a configuração ideal de pontos para todas as equipes empatadas é 12. Assim podemos começar a comparar com os outros resultados como: 5 empates total de 13 pontos, 4 empates total de 14 pontos, 3 empates total de 15 pontos e assim por diante.
Se você olhar a tabela acima perceberá que para 5 empates em 6 partidas teríamos essa configuração de pontos possivelmente para cada equipe. Não é necessário sabermos qual equipe ficará com 5 pontos, ou qual termina com 2 pontos ou 3 pontos, basta sabermos a configuração do resultado e distribuição da tabela. Para essa configuração o total de empates é 5 ( CINCO).
RESPOSTA: 5 EMPATES
4. Marcela quer fazer um jogo de tabuleiro
para a gincana da escola. Ela, então, corta
um retângulo de papel com laterais de 1
decímetro, onde desenha quadrados, também de 1 decímetro, alinhados, e numera-
-os a partir de 1. Quando dobra esse retângulo ao meio, percebe que o quadradinho
com o número 19 ficou em cima do que tem
o número 6. Sabendo que os quadrados se
encaixaram perfeitamente no retângulo,
qual é o comprimento desse retângulo em
decímetros?
RESOLUÇÃO: Se colocarmos em uma tabela na ordem decrescente os números começando pelo 6 e 19 que estão na mesma direção teremos uma ideia de quantos quadradinhos de 1 decímetros teremos.
Se nós somássemos o total de pontos de todas as equipes juntas teríamos um total de 12 pontos. Conclusão: a configuração ideal de pontos para todas as equipes empatadas é 12. Assim podemos começar a comparar com os outros resultados como: 5 empates total de 13 pontos, 4 empates total de 14 pontos, 3 empates total de 15 pontos e assim por diante.
Se você olhar a tabela acima perceberá que para 5 empates em 6 partidas teríamos essa configuração de pontos possivelmente para cada equipe. Não é necessário sabermos qual equipe ficará com 5 pontos, ou qual termina com 2 pontos ou 3 pontos, basta sabermos a configuração do resultado e distribuição da tabela. Para essa configuração o total de empates é 5 ( CINCO).
RESPOSTA: 5 EMPATES
4. Marcela quer fazer um jogo de tabuleiro
para a gincana da escola. Ela, então, corta
um retângulo de papel com laterais de 1
decímetro, onde desenha quadrados, também de 1 decímetro, alinhados, e numera-
-os a partir de 1. Quando dobra esse retângulo ao meio, percebe que o quadradinho
com o número 19 ficou em cima do que tem
o número 6. Sabendo que os quadrados se
encaixaram perfeitamente no retângulo,
qual é o comprimento desse retângulo em
decímetros?
RESOLUÇÃO: Se colocarmos em uma tabela na ordem decrescente os números começando pelo 6 e 19 que estão na mesma direção teremos uma ideia de quantos quadradinhos de 1 decímetros teremos.
 RESPOSTA : 24 DECÍMETROS
5. Certo dia sentei em um banco do prédio onde moro e fiquei a observar o zelador limpando as janelas dos apartamentos
de modo bastante aleatório. Primeiro ele
estava no degrau do meio da escada, depois subiu 5 degraus, em seguida desceu
4 degraus. Um pouco depois, ele subiu 10
degraus e parou um pouco para descansar.
Depois disso, ele subiu os últimos 4 degraus
da escada e foi para o telhado do prédio,
provavelmente para conferir a caixa-d’água.
Quantos degraus tinha a escada usada pelo
zelador?
RESOLUÇÃO: Primeiro vamos imaginar que o meio da escada é 1/2. pois tudo que é representado como metade é sempre dividido por dois. Agora ele subiu 5 e desceu 4, então temos na verdade mais 1 degrau. Depois ele subiu 10 e parou e depois subiu mais 4 degraus dando um total de 15 degraus ao todo. Agora podemos montar a nossa equação. 1/2 = 15/X . Resolvendo a equação teremos 30 degraus ao todo porém ainda não é a nossa resposta.
Lembra do degrau do meio? Pois é. Falta contarmos com ele. Então teremos 31 Degraus ao todo. Essa é nossa resposta certa.
RESPOSTA 31 DEGRAUS
Continuamos resolvendo Problemas envolvendo números inteiros
RESPOSTA : 24 DECÍMETROS
5. Certo dia sentei em um banco do prédio onde moro e fiquei a observar o zelador limpando as janelas dos apartamentos
de modo bastante aleatório. Primeiro ele
estava no degrau do meio da escada, depois subiu 5 degraus, em seguida desceu
4 degraus. Um pouco depois, ele subiu 10
degraus e parou um pouco para descansar.
Depois disso, ele subiu os últimos 4 degraus
da escada e foi para o telhado do prédio,
provavelmente para conferir a caixa-d’água.
Quantos degraus tinha a escada usada pelo
zelador?
RESOLUÇÃO: Primeiro vamos imaginar que o meio da escada é 1/2. pois tudo que é representado como metade é sempre dividido por dois. Agora ele subiu 5 e desceu 4, então temos na verdade mais 1 degrau. Depois ele subiu 10 e parou e depois subiu mais 4 degraus dando um total de 15 degraus ao todo. Agora podemos montar a nossa equação. 1/2 = 15/X . Resolvendo a equação teremos 30 degraus ao todo porém ainda não é a nossa resposta.
Lembra do degrau do meio? Pois é. Falta contarmos com ele. Então teremos 31 Degraus ao todo. Essa é nossa resposta certa.
RESPOSTA 31 DEGRAUS
Continuamos resolvendo Problemas envolvendo números inteiros
 Resposta: 13 poleadas
2. Em um porto, dois homens estão erguendo um contêiner com o auxílio de um sistema
de cabos e roldanas, como mostra a figura a seguir. Se um deles puxar 15 metros de cabo, e o outro puxar 25 metros, quantos metros o contêiner será erguido?
Resposta: 13 poleadas
2. Em um porto, dois homens estão erguendo um contêiner com o auxílio de um sistema
de cabos e roldanas, como mostra a figura a seguir. Se um deles puxar 15 metros de cabo, e o outro puxar 25 metros, quantos metros o contêiner será erguido?
 Resolução: Sabendo que temos dois operários puxando o contêiner faremos o seguinte chamaremos os dois operários de “2x” sendo que um
x= 15 metros e o outro operário de x= 25 metros. Vamos somar os dois ai teremos 2x = 40 metros. Agora dividiremos por dois a equação:
x = 40 / 2 que dará x = 20 metros. Essa é a resposta, 20 metros.
3. Em uma competição de sinuca com quatro duplas participantes, cada dupla jogava uma
vez contra cada uma das outras duplas. Se um confronto acabasse empatado, cada equipe
receberia 1 ponto; do contrário, a dupla vencedora receberia 3 pontos, e a perdedora não pontuaria. A seguir, temos a tabela que mostra o total de pontos obtidos pelas duplas após todos
os confrontos:
Resolução: Sabendo que temos dois operários puxando o contêiner faremos o seguinte chamaremos os dois operários de “2x” sendo que um
x= 15 metros e o outro operário de x= 25 metros. Vamos somar os dois ai teremos 2x = 40 metros. Agora dividiremos por dois a equação:
x = 40 / 2 que dará x = 20 metros. Essa é a resposta, 20 metros.
3. Em uma competição de sinuca com quatro duplas participantes, cada dupla jogava uma
vez contra cada uma das outras duplas. Se um confronto acabasse empatado, cada equipe
receberia 1 ponto; do contrário, a dupla vencedora receberia 3 pontos, e a perdedora não pontuaria. A seguir, temos a tabela que mostra o total de pontos obtidos pelas duplas após todos
os confrontos:
 Número 1: total de confrontos 6 partidas.
agora vamos partir para o Número 2: Possíveis resultados para cada equipe
Número 1: total de confrontos 6 partidas.
agora vamos partir para o Número 2: Possíveis resultados para cada equipe agora que sabemos os números possíveis de resultados para cada equipe somamos os pontos. Veja os exemplos ao lado. primeiro temos os possíveis resultados de três vitórias para uma determinada equipe logo essa equipe faturaria 3 pontos por cada vitória dando um total de 9 pontos. Também temos o resultado de três derrotas dando um total de zero pontos. Temos também o resultado de três empates dando um total de 3 pontos pois cada empate lhe daria 1 ponto…e assim montamos os diversos resultados possíveis como você pode vê ao lado.
Número 3: Comparamos os possíveis resultados com os resultados da tabela das equipes e excluímos alguns resultados.
agora que sabemos os números possíveis de resultados para cada equipe somamos os pontos. Veja os exemplos ao lado. primeiro temos os possíveis resultados de três vitórias para uma determinada equipe logo essa equipe faturaria 3 pontos por cada vitória dando um total de 9 pontos. Também temos o resultado de três derrotas dando um total de zero pontos. Temos também o resultado de três empates dando um total de 3 pontos pois cada empate lhe daria 1 ponto…e assim montamos os diversos resultados possíveis como você pode vê ao lado.
Número 3: Comparamos os possíveis resultados com os resultados da tabela das equipes e excluímos alguns resultados.  Agora vamos excluir e ficar apenas com os resultados que possui o total de pontos para cada equipe. Exemplo: a equipe “A” possui 5 pontos, então só existe uma possibilidade de resultado para esta equipe que seria uma vitória e dois empates. A mesma coisa seria para a equipe “D” que possui 2 pontos, então a única situação que lhe daria esses dois pontos seria dois empates e uma derrota e assim por diante.
Número 4: Vamos agora montar uma tabela com os possíveis pontos e comparar o total de partidas com o total possível de empates. Por exemplo: se todas as equipes empassem então elas só teriam ganhado um ponto por partida e teriam no final de uma rodada um total de 3 pontos cada equipe.
Agora vamos excluir e ficar apenas com os resultados que possui o total de pontos para cada equipe. Exemplo: a equipe “A” possui 5 pontos, então só existe uma possibilidade de resultado para esta equipe que seria uma vitória e dois empates. A mesma coisa seria para a equipe “D” que possui 2 pontos, então a única situação que lhe daria esses dois pontos seria dois empates e uma derrota e assim por diante.
Número 4: Vamos agora montar uma tabela com os possíveis pontos e comparar o total de partidas com o total possível de empates. Por exemplo: se todas as equipes empassem então elas só teriam ganhado um ponto por partida e teriam no final de uma rodada um total de 3 pontos cada equipe. Se nós somássemos o total de pontos de todas as equipes juntas teríamos um total de 12 pontos. Conclusão: a configuração ideal de pontos para todas as equipes empatadas é 12. Assim podemos começar a comparar com os outros resultados como: 5 empates total de 13 pontos, 4 empates total de 14 pontos, 3 empates total de 15 pontos e assim por diante.
Se você olhar a tabela acima perceberá que para 5 empates em 6 partidas teríamos essa configuração de pontos possivelmente para cada equipe. Não é necessário sabermos qual equipe ficará com 5 pontos, ou qual termina com 2 pontos ou 3 pontos, basta sabermos a configuração do resultado e distribuição da tabela. Para essa configuração o total de empates é 5 ( CINCO).
RESPOSTA: 5 EMPATES
4. Marcela quer fazer um jogo de tabuleiro
para a gincana da escola. Ela, então, corta
um retângulo de papel com laterais de 1
decímetro, onde desenha quadrados, também de 1 decímetro, alinhados, e numera-
-os a partir de 1. Quando dobra esse retângulo ao meio, percebe que o quadradinho
com o número 19 ficou em cima do que tem
o número 6. Sabendo que os quadrados se
encaixaram perfeitamente no retângulo,
qual é o comprimento desse retângulo em
decímetros?
RESOLUÇÃO: Se colocarmos em uma tabela na ordem decrescente os números começando pelo 6 e 19 que estão na mesma direção teremos uma ideia de quantos quadradinhos de 1 decímetros teremos.
Se nós somássemos o total de pontos de todas as equipes juntas teríamos um total de 12 pontos. Conclusão: a configuração ideal de pontos para todas as equipes empatadas é 12. Assim podemos começar a comparar com os outros resultados como: 5 empates total de 13 pontos, 4 empates total de 14 pontos, 3 empates total de 15 pontos e assim por diante.
Se você olhar a tabela acima perceberá que para 5 empates em 6 partidas teríamos essa configuração de pontos possivelmente para cada equipe. Não é necessário sabermos qual equipe ficará com 5 pontos, ou qual termina com 2 pontos ou 3 pontos, basta sabermos a configuração do resultado e distribuição da tabela. Para essa configuração o total de empates é 5 ( CINCO).
RESPOSTA: 5 EMPATES
4. Marcela quer fazer um jogo de tabuleiro
para a gincana da escola. Ela, então, corta
um retângulo de papel com laterais de 1
decímetro, onde desenha quadrados, também de 1 decímetro, alinhados, e numera-
-os a partir de 1. Quando dobra esse retângulo ao meio, percebe que o quadradinho
com o número 19 ficou em cima do que tem
o número 6. Sabendo que os quadrados se
encaixaram perfeitamente no retângulo,
qual é o comprimento desse retângulo em
decímetros?
RESOLUÇÃO: Se colocarmos em uma tabela na ordem decrescente os números começando pelo 6 e 19 que estão na mesma direção teremos uma ideia de quantos quadradinhos de 1 decímetros teremos.
 RESPOSTA : 24 DECÍMETROS
5. Certo dia sentei em um banco do prédio onde moro e fiquei a observar o zelador limpando as janelas dos apartamentos
de modo bastante aleatório. Primeiro ele
estava no degrau do meio da escada, depois subiu 5 degraus, em seguida desceu
4 degraus. Um pouco depois, ele subiu 10
degraus e parou um pouco para descansar.
Depois disso, ele subiu os últimos 4 degraus
da escada e foi para o telhado do prédio,
provavelmente para conferir a caixa-d’água.
Quantos degraus tinha a escada usada pelo
zelador?
RESOLUÇÃO: Primeiro vamos imaginar que o meio da escada é 1/2. pois tudo que é representado como metade é sempre dividido por dois. Agora ele subiu 5 e desceu 4, então temos na verdade mais 1 degrau. Depois ele subiu 10 e parou e depois subiu mais 4 degraus dando um total de 15 degraus ao todo. Agora podemos montar a nossa equação. 1/2 = 15/X . Resolvendo a equação teremos 30 degraus ao todo porém ainda não é a nossa resposta.
Lembra do degrau do meio? Pois é. Falta contarmos com ele. Então teremos 31 Degraus ao todo. Essa é nossa resposta certa.
RESPOSTA 31 DEGRAUS
Continuamos resolvendo Problemas envolvendo números inteiros
RESPOSTA : 24 DECÍMETROS
5. Certo dia sentei em um banco do prédio onde moro e fiquei a observar o zelador limpando as janelas dos apartamentos
de modo bastante aleatório. Primeiro ele
estava no degrau do meio da escada, depois subiu 5 degraus, em seguida desceu
4 degraus. Um pouco depois, ele subiu 10
degraus e parou um pouco para descansar.
Depois disso, ele subiu os últimos 4 degraus
da escada e foi para o telhado do prédio,
provavelmente para conferir a caixa-d’água.
Quantos degraus tinha a escada usada pelo
zelador?
RESOLUÇÃO: Primeiro vamos imaginar que o meio da escada é 1/2. pois tudo que é representado como metade é sempre dividido por dois. Agora ele subiu 5 e desceu 4, então temos na verdade mais 1 degrau. Depois ele subiu 10 e parou e depois subiu mais 4 degraus dando um total de 15 degraus ao todo. Agora podemos montar a nossa equação. 1/2 = 15/X . Resolvendo a equação teremos 30 degraus ao todo porém ainda não é a nossa resposta.
Lembra do degrau do meio? Pois é. Falta contarmos com ele. Então teremos 31 Degraus ao todo. Essa é nossa resposta certa.
RESPOSTA 31 DEGRAUS
Continuamos resolvendo Problemas envolvendo números inteiros 